- 拉格朗日插值
- 均差与牛顿插值多项式
- 埃尔米特插值
- 分段低次插值
- 三次样条插值
有些老师如同大山一样压抑着学生。
华中师范大学真是太多好老师了,可惜这辈子,在本科期间是无缘再见了。
潘老师的学习建议
重基础,多练习,勤思考
I hear and I forget, I see and I remember, I do and I understand.
- 注意掌握各种数值方法的思想和原理,而不是死记硬背
- 注意数值方法的处理技巧,以及与计算机编程的结合(编程实践)
- 注重必要的数值计算训练(必要的手算推导能力)
- 要重视算法的误差分析、收敛性和稳定性
纸上得来终觉浅,绝知此事要躬行。
问题的提出
白话:根据有限数据来推测未知点的值
插值函数:
P(xi)=yi(i=0,1,⋯,n)
插值多项式:
P(x)=a0+a1x+⋯+anxn
确定曲线(插值函数)使其通过插值点,用它近似表示数据的理想函数。
多项式插值
给定n+1个点,求次数不超过n的多项式。 ai为未知数
⎩⎨⎧a0+a1x0+⋯+anx0n=y0a0+a1x1+⋯+anx1n=y1...a0+a1xn+⋯+anxnn=yn
化成范德蒙矩阵,其行列式值不为零,解唯一。
行列式值与解的关系 待补充
拉格朗日插值
线性插值
只有两个节(数据)点(xk,yk),(xk+1,yk+1)
P(x)=a0+a1x=L1(x)(线性插值)
要求插值函数上的值与节点值严格一致,在图像上显示出来就是一条直线,其斜率为:
k=xk+1−xkyk+1−yk
转化成:
L1(x)=yklk(x)+yk+1lk+1(x)
其中:
lk(x)=xk−xk+1x−xk+1lk+1(x)=xk+1−xkx−xk
lk(x),lk+1(x)为线性插值基函数,在节点上满足:
lk(xk)=1lk(xk+1)=0lk+1(xk)=0lk+1(xk+1)=1
习题1: (1,0) (2,4)
l1=2−1x−1=x−1l2=1−2x−2=2−x
l1(x)=0+4x−4=4x−4
抛物插值
有三个节点时:
P(x)=a0+a1x+a2x2=L2(x)(抛物插值)
进而化简得到基函数:下面节点减去所有其他的点,上面用x替换节点
L2(x)=yk−1lk−1(x)+yklk(x)+yk+1lk+1(x)
其中:
lk−1(x)=(xk−1−xk)(xk−1−xk+1)(x−xk)(x−xk+1)
基函数序数与x序数的关系:相等为1,不相等为0。
lk−1(xk−1)=1lk−1(xk)=0lk−1(xk+1)=0...
习题2: (0,1) (1,2) (2,3)
l1(x)=(0−1)(0−2)(x−1)(x−2)...
L2(x)=l1(x)y1+...
拉格朗日插值多项式
当节点数n比3大时
Ln(xj)=k=0∑nyklk(xj)=yj(j=0,1,⋯,n)
n次插值基函数性质:
lj(xk)={10k=jk=j
lk(x)=(xk−x0)⋯(xk−xk−1)(xk−xk+1)⋯(xk−xn)(x−x0)⋯(x−xk−1)(x−xk+1)⋯(x−xn)
引入记号:
ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)
所以:
ωn+1′(xk)=(xk−x0)⋯(xk−xk−1)(xk−xk+1)⋯(xk−xn)
于是公式(3.5)可以化简为:
Ln(x)=k=0∑nyk(x−xk)ωn+1′(xk)ωn+1(x)
特别篇- 拉格朗日插值的C++ 实现
题目:求以下数据的以多项式为基底、以拉格朗日插值多项式为基底、以牛顿插值多项式为基底 的二次插值多项式:
| f(x) |
0 |
-3 |
4 |
| x |
1 |
-1 |
2 |
解答:
-
多项式插值:
直接设未知数,代入解方程即可,可以求得:
F(x)=6−20+9x+11x2
- 拉格朗日插值多项式
L0(x)L1(x)L2(x)∴L2(x)=21−2x2=62−3x+x2=3−1+x2=6−14+9x+5x2
-
牛顿插值多项式
设此二次多项式为:
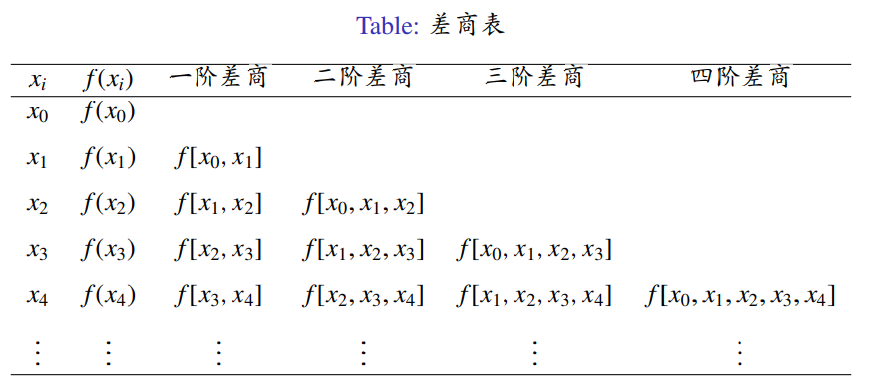
P2(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)
差商表如下:
| xi |
f(xi) |
一阶差商 |
二阶差商 |
| 1 |
0 |
|
|
| -1 |
-3 |
23 |
|
| 2 |
4 |
37 |
65 |
代入可以求得P2(x)为:
P2(x)=6−14+9x+5x2
可见在最高阶次为2的情形下,拉格朗日插值与牛顿插值 得到的结果形式上一致
-
编程实现:
01_Lagrange.c1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include<stdio.h>
float lagrange(float x[],float y[],float xx,int n)
{
int i,j;
float *a,yy=0;
a=new float[n];
for(i=0;i<=n-1;i++)
{
a[i]=y[i];
for(j=0;j<=n-1;j++)
if(j!=i)a[i]*=(xx-x[j])/(x[i]-x[j]);
yy+=a[i];
}
delete a;
return yy;
}
int main()
{
float y[3]={0, -3, 4};
float x[3]={1, -1, 2};
float xx1=1,xx2=0,xx3=2,yy1,yy2,yy3;
yy1=lagrange(x,y,xx1,3);
yy2=lagrange(x,y,xx2,3);
yy3=lagrange(x,y,xx3,3);
printf("x1=%-20f,y1=%f\n",xx1,yy1);
printf("x2=%-20f,y2=%f\n",xx2,yy2);
printf("x3=%-20f,y3=%f\n",xx3,yy3);
return 0;
}
|
输出结果1
2
3
| x1=1.000000 ,y1=0.000000
x2=0.000000 ,y2=-2.333333
x3=2.000000 ,y3=4.000000
|
可见与理论结果是很相符合的。
插值余项与误差估计
罗尔定理
余项定义:
Rn(x)=f(x)−Ln(x)
Rn(x)=f(x)−Ln(x)=(n+1)!f(n+1)(ξ)ωn+1(x)
牛顿插值
为何要用牛顿插值法?
拉格朗日插值与插值节点的依赖性太大,用牛顿插值法可以逐次进行插值。
将拉格朗日线性插值看作零次插值的修正;线性插值看作抛物插值的修正;…
差商(微商的离散形式,也叫均差):
- 点 x0,x1 互异,定义函数 f(x) 的一阶均差
f[x0,x1]=x1−x0f(x1)−f(x0)
- 点 x0,x1,x2 互异,定义 f(x) 的二阶均差
f[x0,x1,x2]=x2−x0f[x1,x2]−f[x0,x1]
- 点 x0,x1,…,xk 互异,定义 f(x) 的 n 阶均差定义为
f[x0,x1,…,xk]=xk−x0f[x1,…,xk]−f[x0,…,xk−1]
f[xi,xi+1,⋯,xi+k]=xi+k−xif[xi+1,xi+2,⋯,xi+k]−f[xi,xi+1,⋯,xi+k−1]
差商的性质
-
k阶差商
f[x0,x1,⋅⋅⋅,xk]=j=0∑kωk+1′(xj)f(xj)
-
差商与其所含节点的排列次序无关,即
f[xi,xi+1]=f[xi+1,xi]
-
设f(x)在包含互异节点x0,x1,⋅⋅⋅,xn的闭区间[a,b]上有n阶导数,则
f[x0,x1,⋅⋅⋅,xn]=n!fn(ξ)ξ∈(a,b)

牛顿插值多项式
2021-10-16 12:31:19
不学了!!!我要去收拾东西,晚上再坐上32个小时的火车,去向不可知的远方。楼下母亲快把饭做好了,饿!饿!饿!
回到学校再来过!!!
依次迭代可以得到,牛顿插值多项式的形式。把 x 看成一个点,由均差定义得
f(x)=f(x0)+(x−x0)f[x,x0]f[x,x0]=f[x0,x1]+(x−x1)f[x,x0,x1].f[x,x0,x1]=f[x0,x1,x2]+(x−x2)f[x,x0,x1,x2]……f[x,x0,…,xn−1]=f[x0,…,xn]+(x−xn)f[x,x0,…,xn]
把后一式依次代入前一式得
其中 f(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,x1,⋯,xn](x−x0)⋯(x−xn−1)+f[x,x0,⋯,xn]ωn+1(x)=Nn(x)+Rn(x)ωn+1(x)=(x−x0)(x−x1)⋯(x−xn).
简化一下,于是得到牛顿插值多项式:
Nn(x)=R~n(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn−1)f[x,x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn)
称Nn(x)为n次牛顿插值多项式,R~n(x)为牛顿型插值余项。
- 插值多项式存在且唯一:Pn(x)≡Ln(x)
差分形式
步长:等距节点xk=x0+kh (k=0,1,…,n)
称Δfk=fk+1−fk为一阶差分
Δfk=fk+1−fk
f[x0,x1,⋯,xk]=k!hkΔky0,k=1,2,⋯,nf[xn,xn−1,⋯,xn−k]=k!hk∇kyn,k=1,2,⋯,n
-
差分与导数的关系
Δnyo=hnf(n)(ξ) ξ∈(x0,xn)
-
牛顿向前插值多项式
Pn(x0+th)=f(x0)+tΔy0+2!t(t−1)Δ2y0+⋯+n!t(t−1)⋯(t−n+1)Δny0
其余项为:
Rn(x0+th)=n!t(t−1)⋯(t−n+1)hn+1f(n+1)(ξ)ξ∈(x0,xn)
课后作业
第一题
已知数据:
xiui111.5222.22.522.0438.3651.1
使用拉格朗日和一般多项式方法进行插值。
解:
- 一般多项式插值由题可得多项式为:
a_0+a_1+a_2+a_3+a_4=11.5 \
a_0+a_1 2+a_2 4+a_{33} 8+a_4 \times 16=22.4 \
a_{10}+a_1 2.5+a_2 .6 .25+a_3 \times 15.625+a_4 \times 38.0625=22.0 \
a_0+a_1 \times 4+a_2 \times 16+a_3 \times 64+a_4 \times 2156=38.3 \
a_0+a_1 \times 6+a_2 \times 36+a_3 \times 216+a_4 \times 1286=51.1
\end{array}\right.
其矩阵形式为:
\left[\begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \
1 & 2 & 4 & 8 & 16 \
1 & 25 & 6.25 & 15.625 & 31.0625 \
1 & 4 & 16 & 64 & 256 \
1 & 6 & 36 & 216 & 1286
\end{array}\right]\left[\begin{array}{l}
a_0 \
a_1 \
a_2 \
a_3 \
a_4
\end{array}\right]=\left[\begin{array}{c}
11.5 \
22.2 \
22.0 \
38.3 \
51.1
\end{array}\right]
求解可得:
\left{\begin{array}{l}
a_0=-60.26 \
a_1=10 9.205 \
a_2=-43.3825 \
a_3=7.1275 \
a_4=-1.215
\end{array}\right.
所以一般多项式的插值公式为:
u_1(x)=\sum_n^R a_i x=-1.215 x^4+7.1275 x^3-43.8325 x^2+10 9. 205 x-60.26
2. 拉格朗日插值
设该插值多项式为$u(x)$则
\begin{aligned}
\mu(x)&=\sum_{i=1}^n u P_i(x)\=
&11.5 \times \frac{(x-2)(x-2.5)(x-4)(x-6)}{(-1) \times(-1.5) \times(-3) \times(-5)}+22.2 \times \frac{(x-1)(x-2.5)(x-4)(x-6)}{1 \times(-0.5) \times(-2) \times(-4)}\&+22 \times \frac{(x-1)(x-2)(x-4)(x-6)}{1.5 \times 0.5 \times(-1.5) \times(-3.5)} +38.3 \times \frac{(x-1)(x-2)(x-2.5)(x-6)}{3 \times 2 \times 1.5 \times(-2)}\ &+51.1 \times \frac{(x-1)(x-2)(x-2.5)(x-4)}{5 \times 4 \times 3.5 \times 2}\=
&0.51 x(x-2)(x-2.5)(x-4)(x-6)+(-5.55)(x-1)(x-2.5)(x-4)(x-6)\ &+5.58(x-1)(x-2)(x-4)(x+6)
+(-2.12)(x-1)(x-2)(x-2.5)(x-6)\ & +0.365(x-1)(x-2)(x-2.5)(x-4)
\end
### 第二题
用雅可比迭代求解方程组。(初始向量:$\boldsymbol{x}^{(0)}=\left[\begin{array}{lll}0 & 0 & 0\end{array}\right]^{\mathrm{T}}$)
\left[\begin{array}{ccc}
1 & 2 & -2 \
1 & 1 & 1 \
2 & 2 & 1
\end{array}\right]\left[\begin{array}{l}
x_1 \
x_2 \
x_3
\end{array}\right]=\left[\begin{array}{l}
1 \
3 \
5
\end{array}\right]
解:由题可得:
\left{ \begin{aligned}
&x_1^{(k+1)}=1-2 x_2^{(k)}+2 x_3^{(k)} \
&x_2{(k+1)}=3-x_1-x_3^{(k)} \
&x_3^{(k+1)}=5-2 x^{(k)}-2 x_2^{(k)}
\end{aligned}\right.
取初始向量:$\boldsymbol{x}^{(0)}=\left[\begin{array}{lll}0 & 0 & 0\end{array}\right]^{\mathrm{T}}$,则有:
\left{ \begin{aligned}
&x^{(1)}=\left[\begin{array}{lll}
1 & 3 & 5
\end{array}\right]^{\top} \
&x^{(2)}=\left[\begin{array}{lll}
5 & -3 & -3
\end{array}\right]^{\top} \
&x^{(3)}=\left[\begin{array}{lll}
1 & 1 & 1
\end{array}\right]^{\top} \
&x^{(4)}=\left[\begin{array}{lll}
1 & 1 & 1
\end{array}\right]^{\top} \
\end{aligned}\right.
因为:$\left\|x^{(3)}-x^{(4)}\right\|<0.01$ 在误差允许范围内所以$[1,1,1]$为最终解。 ### 第三题 试实现高斯-赛德尔迭代算法的程序化,并利用程序求解方程组。 \left[\begin{array}{ccc}
8 & -3 & 2 \
4 & 11 & -1 \
6 & 3 & 12
\end{array}\right]\left[\begin{array}{l}
x_1 \
x_2 \
x_3
\end{array}\right]=\left[\begin{array}{l}
20 \
33 \
36
\end{array}\right]
解:根据算法得到如下程序<!−−code2−−>输出结果为<!−−code3−−>