时域响应分析

参考：线性系统的时域分析与校正

时间响应分类

1. 瞬态响应： 从初始态到接近稳态的响应。反映了过渡过程的平稳性和快速性。

2. 稳态响应：t趋于无穷大时固定下来的输出状态，不一定是常数。与系统准确性（精度）密切相关。

   时域分析 是根据微分方程，利用拉氏变换直接求出系统的时间响应，然后按照响应曲线来分析系统的性能。

典型输入信号

1. 阶跃信号(a=1,单位阶跃信号)

   $$x_i(t)= \begin{cases} a & t>0 \\ 0 & t<0 \end{cases} \tag{3.1}$$

2. 斜坡信号(a=1,单位斜坡信号)

   $$x_i(t)= \begin{cases} at & t>0 \\ 0 & t<0 \end{cases} \tag{3.2}$$

3. 加速度信号(a=1/2,单位加速度信号)

   $$x_i(t)= \begin{cases} at^2 & t>0 \\ 0 & t<0 \end{cases}\tag{3.3}$$

4. 脉冲信号(面积为a)

   $$x_i(t)= \begin{cases} \displaystyle \lim_{t_0\to 0}\frac{a}{t_0} & 0<t<t_0 \\ 0 & t<0\ or\ t>t_0 \end{cases}\tag{3.4}$$

   当系统输入为单位脉冲函数时，其输出响应称为脉冲响应函数。由于δ函数的拉氏变换等于1，因此系统传递函数即为脉冲响应函数的象函数。

   当系统输入任一时间函数时，可以将输入信号分割为n个脉冲(与微分类似)，可以得到其输出响应为输入信号与脉冲响应函数的卷积。

5. 正弦函数

   $$x_i(t)= \begin{cases} asin(\omega t) & t>0 \\ 0 & t<0 \end{cases}\tag{3.5}$$

   选择哪种函数作为典型输入信号，应视不同系统的具体工作情况而定。

一阶系统

能用能够用一阶微分方程描述的系统，它的典型形式是一阶惯性环节。

$$\frac{X_0(s)}{X_i(s)}=\frac{1}{Ts+1}\tag{3.6}$$

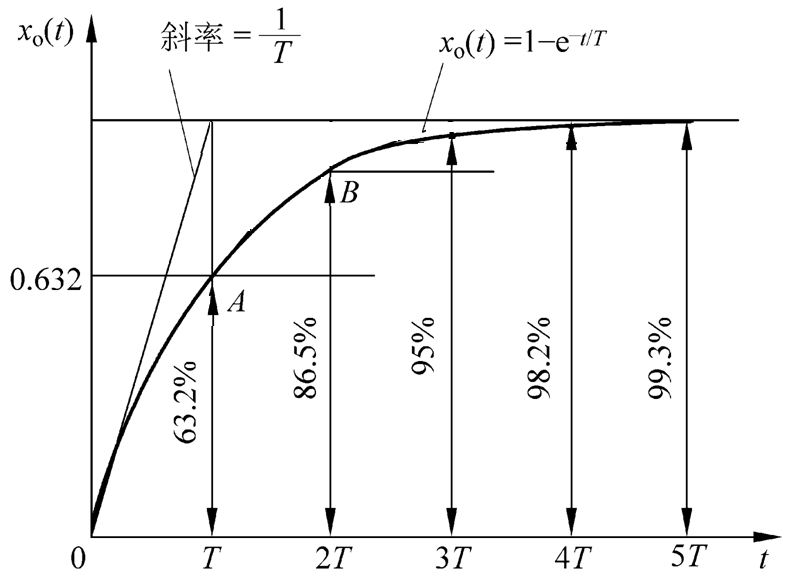
单位阶跃输入

• 切线斜率确定

• 时间常数越大，反应越慢

  • 稳定，无振荡；

  • 经过时间 T 曲线上升到 0.632 的高度；

  • 调整时间为 (3～4)T ；

  • 在 t = 0 处，响应曲线的切线斜率为 1/T；

  • $(-\frac{1}{T}\lg e)t=\lg[1-x_o(t)]$

单位斜坡输入

单位斜坡输入