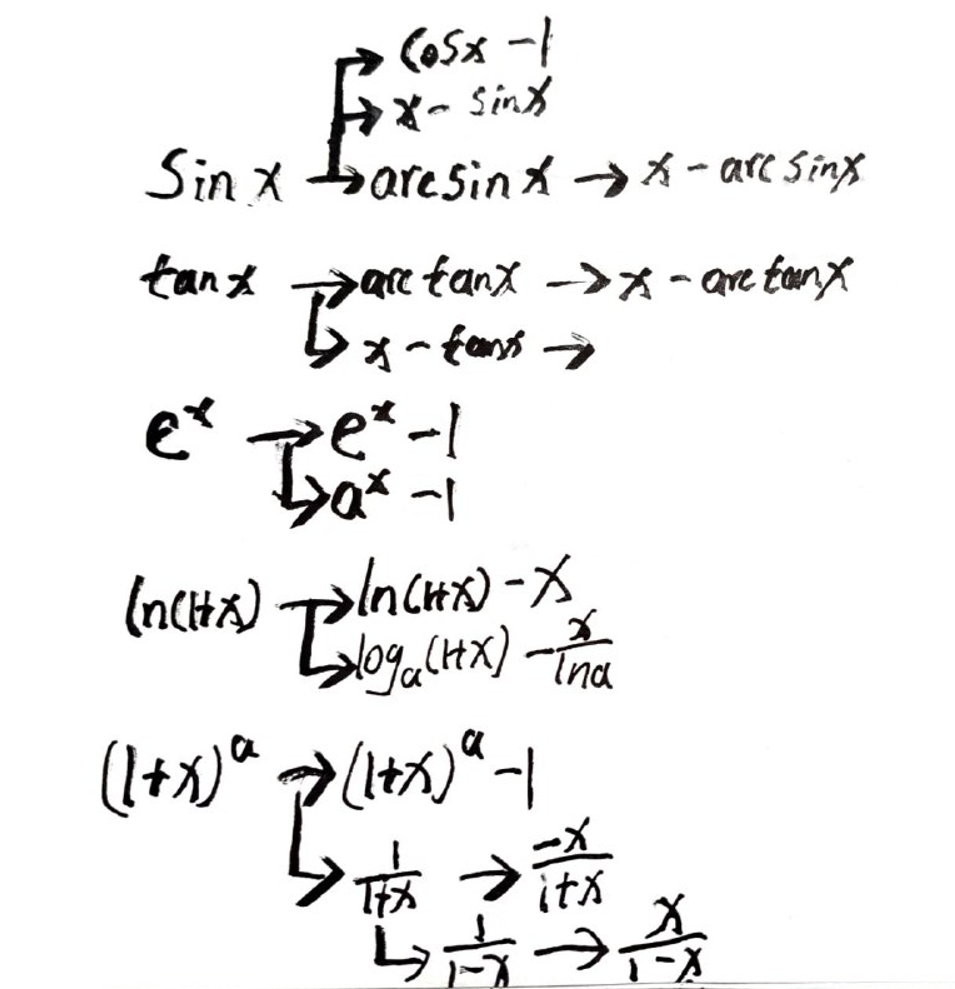极限100/2

泰山之管穿石，单极之绠断干。水非石之钻，索非木之锯，渐靡使之然也。

——东汉·班固《汉书·枚乘传》

本文封面为Rocky Ⅱ^[1]中Rocky下定决心比赛后，早晨疯狂锻炼的场景。有了目标，便要不顾风雨兼程。

楔子

前两天看到 blackpenredpen曹老师 的视频，有感触，觉得对于数学的学习而言，刷题中才能真正学会东西。有些东西，看了不一定理解，理解了不一定会应用，用了不一定真正掌握。做题能很好的杂糅这一切，让理解更深入，记忆更加清晰。

时间线

4-3~

4-6

收集到22个，感觉没得写了。早上偶然看到mdnice群里有人发导数的笔记，然后又翻到了他之前的极限笔记。然而，笔记里第一题我都做的吃力，NND，再看才知晓是Wu老的高数17天。然后找来翻了翻，光极限就讲了57页😮，当然里面方法还是基本方法，但很多都是“稍稍”延伸了几步，却足以让我手足无措。这两天不能放松，好好理理思路。

4-7

要把等价无穷小推导一遍，不然太不好记了。

4-9

利用泰勒展开式推导出所有常见无穷小（4 $\to$ 50）

4-15

累了，多巴胺业已耗尽，五十道，了了之。

初出茅庐

这一部分有27道例题，主要介绍极限计算的基本方法。

$$\begin{equation} \lim_{n\to \infty}\ \frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+\dots \frac{1}{\sqrt{n^2+n}} \end{equation}$$

bg

提示：利用夹逼定理（🗣️哪—里—跑—）

$$\frac{1*n}{\sqrt{n^2+1}}\le b_n \le \frac{1*n}{\sqrt{n^2+n}}$$

quation}
\lim _{x \rightarrow 0} \frac{\ln \left(1+4 x^{2}\right)}{\sin x^{2}}
\end

$$color$$

提示：等价无穷小

folding (🥕)}\sim \ln(1+🥕)

$$\begin{aligned} & \lim _{x \rightarrow 0} \frac{\ln \left(1+4 x^{2}\right)}{\sin x^{2}} \\ &= \frac{4 x^{2}}{x^{2}} \\ &=\ 4 \end{aligned}$$

\befolding_{x \rightarrow 0} x^{3} \sin \frac{1}{x^{3}}
\end

$$bg$$

提示：注意等价无穷小的条件

$$folding,\ x^3\text{为无穷小},|\sin{\frac{1}{x^3}}|\le 1 \\ {\color{blue} \text{无穷小与有界变量的乘积仍为无穷小}}\\ \therefore \lim _{x \rightarrow 0} x^{3} \sin \frac{1}{x^{3}}= 0$$

\beginfolding_{x \rightarrow 0} \frac{\sin x-\tan x}{x^{3}}
\end

$$bg$$

提示：拼凑等价无穷小

\befoldinglim _{x \rightarrow 0} \frac{\sin x-\tan x}{x^{3}}\\ &=\lim _{x \rightarrow 0} \frac{\sin x\left(1-\frac{1}{\cos x}\right)}{x^{3}} \\ &=\lim _{x \rightarrow 0} \frac{\sin x(\cos x-1)}{x^{3} \cos x} \\ &=\lim _{x \rightarrow 0} \frac{x \cdot\left(-\frac{1}{2} x^{2}\right)}{x^{3}}\\ &=-\frac{1}{2}\end{aligned}

\begin{equation}
\lim _{x \rightarrow 0}\left(1+x e^{x}\right){\frac{1}{x}}
\end

$$bg$$

提示：$1^\infty$常规思路·第一弹

$$\lim_{x\to 0} (1+🥕)^{\frac{1}{🥕}}=e \quad{(🥕\ne0)}$$

\begin{equation}
\lim _{x \rightarrow 0}\left(\frac{1-\tan x}{1+\tan x}\right)^{\frac{1}{-\sin 2 x}}
\end

$$bg$$

提示：$1^\infty$常规思路·第二弹

$$\begin{aligned}&\lim _{x \rightarrow 0}\left(\frac{1-\tan x}{1+\tan x}\right)^{\frac{1}{-\sin 2 x}}\\&=\lim _{x \rightarrow 0}\left(1+(\frac{1-\tan x}{1+\tan x}-1)\right)^{\frac{1}{\frac{1-\tan x}{1+\tan x}-1}\times \frac{-2\tan x}{1+\tan x}\frac{1}{-\sin 2 x}}\\&=\lim _{x \rightarrow 0}e^{ \frac{-2\tan x}{1+\tan x}\frac{1}{-\sin 2 x}}\\&=\lim _{x \rightarrow 0}e^{ \frac{-2 x}{1+\tan x}\frac{1}{- 2 x}}\\&=\lim _{x \rightarrow 0}e^{ \frac{1}{1+\tan x}}\\&=e\end{aligned}$$

\begin{equation}
\lim_{n\to \infty} (\sqrt{n^2+n}-n)
\end

$$bg$$

提示：常规思路：平方差拼凑

$$\begin{aligned}&\lim_{n\to \infty} (\sqrt{n^2+n}-n)\\&=\lim_{n\to \infty} (\frac{\sqrt{n^2+n}-n}{1})\\&=\lim_{n\to \infty} (\frac{n^2+n-n^2}{\sqrt{n^2+n}+n)}\\&=\lim_{n\to \infty} (\frac{n}{\sqrt{n^2+n}+n)}\\&=\lim_{n\to \infty} (\frac{1}{\sqrt{1+\frac{1}{n}}+1})\\&=\frac{1}{2}\\\end{aligned}$$

\begin{equation}
\lim_{x\to \infty} \sqrt{x}(\sqrt{x+2}-\sqrt{x-3})
\end

$$bg$$

提示：常规思路：平方差拼凑

$$\begin{aligned}&\lim_{x\to \infty} \sqrt{x}(\sqrt{x+2}-\sqrt{x-3})\\&=\lim_{x\to \infty} \frac{\sqrt{x}(\sqrt{x+2}-\sqrt{x-3})}{1}\\&=\lim_{x\to \infty} \frac{\sqrt{x}\times 5}{\sqrt{x+2}+\sqrt{x-3})}\\&=\lim_{x\to \infty} \frac{ 5}{\sqrt{1+2/x}+\sqrt{1-3/x})}\\&=\frac{5}{2}\end{aligned}$$

\begin{equation}
\lim _{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{e^{x}-1}\right)
\end

$$bg$$

提示：凑乘积形式，等价无穷小+洛必达

$$\begin{aligned} &\lim _{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{e^{x}-1}\right)\\ &=\lim _{x \rightarrow 0}\left(\frac{e^x-1-x}{(e^x-1)x}\right)\\ &=\lim _{x \rightarrow 0}\left(\frac{e^x-1-x}{x^2}\right)\\ &=\lim _{x \rightarrow 0}\left(\frac{e^x-1}{2x}\right)\\ &=\lim _{x \rightarrow 0}\left(\frac{e^x}{2}\right)\\ &=\frac{1}{2}\end{aligned}$$

\begin{equation}
\lim_{x\to 0} \frac{(x-\sin x) e^{-x2}}{\sqrt{1-x^3}-1}
\end

$$bg$$

提示：等价无穷小替换

$$(1+🥕)^a-1 \sim a🥕$$

$$\begin{aligned}&\lim_{x\to 0} \frac{(x-\sin x) e^{-x^2}}{\sqrt{1-x^3}-1}\\&= \lim_{x\to 0} e^{-x^2}\times \lim_{x\to 0} \frac{x-\sin x}{1/2\times (-x^3)}\\&= -2\times \lim_{x\to 0} \frac{x-\sin x}{x^3}\qquad \text{洛必达法则}\\&= -2\times \lim_{x\to 0} \frac{1-\cos x}{3x^2}\\&= -2\times \lim_{x\to 0} \frac{1/2 \times x^2}{3x^2}\\&=- \frac{1}{3}\end{aligned}$$

\begin{equation}
\lim_{x\to 0} \frac{x-\sin 2x}{x + \sin 5x}
\end

$$bg$$

提示：加减法使用等价无穷小的条件

$\because$ 当 $x \rightarrow 0$ 时, $\sin 2 x \sim 2 x, \sin 5 x \sim 5 x$, 且 $\lim _{x \rightarrow 0} \frac{\sin 2 x}{x}$ $=2 \neq 1, \lim _{x \rightarrow 0} \frac{\sin 5 x}{x}=5 \neq-1$,

满足等价无穷小替换对加减法成立的条件,

$$\therefore \lim _{x \rightarrow 0} \frac{x-\sin 2 x}{x+\sin 5 x}=\lim _{x \rightarrow 0} \frac{x-2 x}{x+5 x}=-\frac{1}{6}$$

\begin{equation}
\lim _{x \rightarrow \infty}\left(\cos \frac{1}{x}\right)^{x{2}}
\end

$$bg$$

提示：$1^{\infty}$型·第三弹

$$\begin{aligned}&\displaystyle \lim _{x \rightarrow \infty}\left(\cos \frac{1}{x}\right)^{x^{2}}\\&=\displaystyle\lim_{x\to \infty}[1+(\frac{1}{\cos x}-1)]^{\frac{1}{\frac{1}{\cos x}-1}\times (\frac{1}{\cos x}-1)\times x^2}\\&=e^{\displaystyle\lim_{x\to \infty}\left(\cos \frac{1}{x}-1\right) x^{2}}\\&=e^{\displaystyle\lim_{x\to \infty} \frac{\cos \frac{1}{x}-1}{\left(\frac{1}{x}\right)^{2}}}\\&=e^{\displaystyle\lim_{x\to \infty} \frac{-\frac{1}{2}\left(\frac{1}{x}\right)^{2}}{\left(-\frac{1}{x}\right)^{2}}}\\&=e^{^{-\frac{1}{2}}}\\&=\frac{1}{\sqrt{e}}\end{aligned}$$

\begin{equation}
\lim _{x \rightarrow \infty} \frac{(x+a)^{x+a}(x+b){x+b}}{(x+a+b)^{2 x+a+b}}
\end

$$bg$$

提示：$1^{\infty}$型·第四弹

$$\begin{aligned}&\lim _{x \rightarrow \infty} \frac{(x+a)^{x+a}(x+b)^{x+b}}{(x+a+b)^{2 x+a+b}}\\&=\lim _{x \rightarrow \infty} \frac{(x+a)^{x+a}}{(x+a+b)^{x+a}} \cdot \frac{(x+b)^{x+b}}{(x+a+b)^{x+b}} \\&=\lim _{x \rightarrow \infty} \frac{1}{\left(1+\frac{b}{x+a}\right)^{x+a}} \cdot \frac{1}{\left(1+\frac{a}{x+b}\right)^{x+b}} \\&=\frac{1}{\mathrm{e}^{b}} \cdot \frac{1}{\mathrm{e}^{a}} \\&=\mathrm{e}^{-(a+b)}\end{aligned}$$

\begin{equation}
\lim _{x \rightarrow 0}\left[\frac{\ln (x+\sqrt{1+x^{{2}})}{x}\right]}{\frac{1}{1-\cos x}}
\end

$$bg$$

提示：$1^{\infty}$型·第五弹，常规思路

$$\begin{aligned}&\lim _{x \rightarrow 0}\left[\frac{\ln \left(x+\sqrt{1+x^{2}}\right)}{x}\right]^{\frac{1}{1-\cos x}}\\&=\lim _{x \rightarrow 0}\left[1+\frac{\ln \left(x+\sqrt{1+x^{2}}\right)-x}{x}\right]^{\frac{1}{1-\cos x}} \\&=\lim _{x \rightarrow 0} e^{\frac{\ln (x + \sqrt{1+x^2})-x}{x(1-\cos x )}}\\\text{幂化简：}&\color{blue}\lim _{x \rightarrow 0} \frac{\ln \left(x+\sqrt{1+x^{2}}\right)-x}{x \cdot \frac{1}{2} x^{2}} \\&\color{blue}=\lim _{x \rightarrow 0} \frac{\frac{1}{\sqrt{1+x^{2}}}-1}{\frac{3}{2} x^{2}} \\&\color{blue}=\lim _{x \rightarrow 0} \frac{-\frac{1}{2} x^{2}}{\frac{3}{2} x^{2}}\\&\color{blue}=-\frac{1}{3}\\\text{原式}&=e^{-\frac{1}{3}}\\\end{aligned}$$

\begin{equation}
\lim _{n \rightarrow \infty}\left(\frac{\pi}{2}-\arctan n\right)^{\frac{1}{\ln n}}
\end

$$bg$$

提示：$1^{\infty}$型·变体，思路还是一样的，幂运算变乘法

$$\begin{aligned}&\lim _{n \rightarrow \infty}\left(\frac{\pi}{2}-\arctan n\right)^{\frac{1}{\ln n}}\\&=\lim _{n \rightarrow \infty}e^{\frac{\ln (\pi /2 - \arctan x)}{\ln x}}\\\text{幂化简：}&\color{blue}\lim _{n \rightarrow \infty} \frac{\ln (\pi /2 - \arctan x)}{\ln x}\\&\color{blue}=\lim _{x \rightarrow+\infty} \frac{\frac{1}{\frac{\pi}{2}-\arctan x} \cdot\left(-\frac{1}{1+x^{2}}\right)}{\frac{1}{x}}\\&\color{blue}=-\lim _{x \rightarrow+\infty} \frac{\frac{1}{x}}{\frac{\pi}{2}-\arctan x} \\&\color{blue}=-\lim _{x \rightarrow+\infty} \frac{-\frac{1}{x^{2}}}{-\frac{1}{1+x^{2}}}\\&\color{blue}=-1\\\text{原式}&=e^{-1}\\\end{aligned}$$

\begin{equation}
\lim_{x\to 0} \frac{1-\cos^2x-\frac{1}{2} x \sin 2x}{x^2(e-1)}
\end

$$bg$$

提示：多次使用洛必达法则

$$\begin{aligned}&\displaystyle \lim_{x\to 0} \frac{1-\cos^2x-\frac{1}{2} x \sin 2x}{x^2(e^{x^2}-1)}\\&=\displaystyle \lim_{x\to 0} \frac{1-\cos^2x-\frac{1}{2} x \sin 2x}{x^2\times x^2}\qquad \text{上下都趋近于0，使用洛必达法则}\\&=\displaystyle \lim_{x\to 0} \frac{2\cos x\sin x-\frac{1}{2}\sin 2x-\cos 2x\times x}{4x^3}\\&=\displaystyle \lim_{x\to 0} \frac{\frac{1}{2}\sin 2x-\cos 2x\times x}{4x^3}\qquad \text{上下都趋近于0，使用洛必达法则}\\&=\displaystyle \lim_{x\to 0} \frac{\cos 2x-\cos 2x+\sin 2x\times 2 x}{12x^2}\\&=\displaystyle \lim_{x\to 0} \frac{ 2x\times 2 x}{12x^2}\\&=\frac{1}{3}\end{aligned}$$

\begin{equation}
\lim _{x\to 0}(\frac{1}{x^{2}-\frac{1}{\sin}2x})
\end

$$bg$$

提示：多次使用洛必达法则

$$\begin{aligned}&\displaystyle\lim _{x\to 0}(\frac{1}{x^2}-\frac{1}{\sin^2x})\\ &=\displaystyle\lim _{x\to 0}\frac{\sin^2x-x^2}{x^2 \sin^2x}\qquad \text{上下都趋近于0，使用洛必达法则}\\ &=\displaystyle\lim _{x\to 0}\frac{\sin 2x-2x}{4x^3}\qquad \text{上下都趋近于0，使用洛必达法则} \\&=\displaystyle\lim _{x\to 0}\frac{2\cos 2x-2}{12x^2} \\&=\displaystyle\lim _{x\to 0}\frac{\cos 2x-1}{6x^2} \\&=\displaystyle\lim _{x\to 0}\frac{\frac{1}{2} (2x)^2}{6x^2}\\&=\frac{1}{3}\end{aligned}$$

\begin{equation}
\lim _{x \rightarrow 0} (\frac{\cos x}{\cos 2x})^{\frac{1}{x2}}
\end

$$bg$$

提示：等价无穷小之 加不反

$$\begin{aligned}&\lim _{x \rightarrow 0} (\frac{\cos x}{\cos 2x})^{\frac{1}{x^2}}\\&=\mathrm{e}^{\displaystyle \lim_{x\to 0} \frac{\left(\frac{\cos x}{\cos 2 x}-1\right)}{x^{2}}}\\&=\mathrm{e}^{\displaystyle \lim_{x\to 0} \frac{\cos x-\cos 2x}{x^2 \cos 2 x}}\\&=\mathrm{e}^{\displaystyle \lim_{x\to 0} \frac{\cos x-\cos 2x}{x^2 }}\\&=\mathrm{e}^{\displaystyle \lim_{x\to 0} \frac{-\sin x+2 \sin 2 x}{2 x}}\qquad \because \lim_{x\to 0}\frac{-\sin x}{2\sin 2x}\ne -1\\&=\mathrm{e}^{\frac{3}{2}} \end{aligned}$$

\begin{equation}
\lim _{x \rightarrow 0} \frac{[\sin x-\sin (\sin x)] \cdot \sin x}{x^{4}}
\end

$$bg$$

提示：等价无穷小+洛必达法则

$$\begin{aligned}&\lim _{x \rightarrow 0} \frac{[\sin x-\sin (\sin x)] \cdot \sin x}{x^{4}} \\&=\lim _{x \rightarrow 0} \frac{\cos x-\cos (\sin x) \cdot \cos x}{3 x^{2}} \\&=\lim _{x \rightarrow 0} \cos x \times \lim _{x \rightarrow 0} \frac{1-\cos (\sin x)}{3 x^{2}} \\&=\lim _{x \rightarrow 0} \frac{\frac{1}{2} \sin ^{2} x}{3 x^{2}} \\&=\lim _{x \rightarrow 0} \frac{1 x^{2}}{6 x^{2}} \\&=\frac{1}{6}\end{aligned}$$

\begin{equation}
\text{求正的常数a与b，使下式成立：}
\lim {x \rightarrow 0} \frac{1}{b x-\sin x} \int^{x} \frac{t^{{2}}{\sqrt{a+t}{2}}} d t=1

\end

$$bg$$

提示：洛必达+等价无穷小,看见积分，必定洛必达。

$$\begin{aligned} \lim _{x \rightarrow 0} \frac{1}{b x-\sin x} \int_{0}^{x} \frac{t^{2}}{\sqrt{a+t^{2}}} d t&=1\\ \lim _{x \rightarrow 0}\frac{ \frac{x^{2}}{\sqrt{a+x^{2}}} }{ {b -\cos x}}&=1\\\lim _{x \rightarrow 0} \frac{1}{\sqrt{a+x^{2}}}\times \lim _{x \rightarrow 0}\frac{ x^{2} }{ {b -\cos x}}&=1\\\frac{1}{\sqrt{a}}\times \lim _{x \rightarrow 0}\frac{ x^{2} }{ {b -\cos x}}&=1\qquad \text{🥝}\\\frac{1}{\sqrt{a}}\times \lim _{x \rightarrow 0}\frac{1}{b} \frac{ x^{2} }{ {1 -\frac{1}{b}\cos x}}&=1\\\frac{1}{\sqrt{a}}\times \lim _{x \rightarrow 0}\frac{1}{b} \frac{ x^{2} }{ \frac{1}{2b}x^2-\frac{1}{b}+1}&=1\\\frac{1}{\sqrt{a}}\times2&=1\\a&=4\\(a=4\to\text{🥝})\Longrightarrow b&=1\end{aligned}$$

\begin{equation}
\lim {x \rightarrow 0} \frac{\int^{x}(x-t) \sin t^{2} \mathrm{~d} t}{\left(x^{2}+x\right)\left(1-\sqrt{1-x^{2}}\right)}
\end

$$bg$$

提示：看见积分，必定洛必达，但也要注意顺序。

$$\begin{aligned}&\lim _{x \rightarrow 0} \frac{\int_{0}^{x}(x-t) \sin t^{2} \mathrm{~d} t}{\left(x^{2}+x^{3}\right)\left(1-\sqrt{1-x^{2}}\right)}\\&=\lim _{x \rightarrow 0} \frac{x \int_{0}^{x} \sin t^{2} \mathrm{~d} t-\int_{0}^{x} t \sin t^{2} \mathrm{~d} t}{\left(x^{2}+x^{3}\right) \cdot \frac{1}{2} x^{2}} \\&=\lim _{x \rightarrow 0} \frac{ x \int_{0}^{x} \sin t^{2} \mathrm{~d} t- \int_{0}^{x} t \sin t^{2} \mathrm{~d} t}{\frac{1}{2} x^{4}} \quad \text{快使用洛必达，哼哼哈嘿！} \\&=\lim _{x \rightarrow 0} \frac{\int_{0}^{x} \sin t^{2} \mathrm{~d} t+x \sin x^{2}-x \sin x^{2}}{2 x^{3}} \\&=\lim _{x \rightarrow 0} \frac{\sin x^{2}}{6 x^{2}}\\&=\frac{1}{6} \end{aligned}$$

\begin{equation}
\lim _{x \rightarrow 0}\left[\frac{1}{e^{x}-1}-\frac{1}{\ln (1+x)}\right]
\end

$$bg$$

提示：等价无穷小+洛必达法则

$$\begin{aligned}&\lim _{x \rightarrow 0}\left[\frac{1}{\mathrm{e}^{x}-1}-\frac{1}{\ln (1+x)}\right]\\&=\lim _{x \rightarrow 0} \frac{\ln (1+x)-\mathrm{e}^{x}+1}{\left(\mathrm{e}^{x}-1\right) \ln (1+x)}\\&=\lim _{x \rightarrow 0} \frac{\ln (1+x)-\mathrm{e}^{x}+1}{x \cdot x} \\& = \lim _{x \rightarrow 0} \frac{\frac{1}{1+x}-\mathrm{e}^{x}}{2 x}\qquad \text{上下都趋近于0，使用洛必达法则} \\&=\frac{1}{2} \lim _{x \rightarrow 0} \frac{1-\mathrm{e}^{x}(1+x)}{x} \cdot \lim _{x \rightarrow 0} \frac{1}{1+x}\\&=\frac{1}{2} \lim _{x \rightarrow 0} \frac{\left(1-\mathrm{e}^{x}(1+x)\right)^{\prime}}{x^{\prime}}\\&=-\frac{1}{2} \lim _{x \rightarrow 0}\left(\mathrm{e}^{x}(2+x)\right)\\&=-1 .\end{aligned}$$

\begin{equation}
\lim _{x \rightarrow 0} \frac{x^{2} \sin \frac{1}{x}}{x+\sin x}
\end

bg

提示：请不要用洛必达！！

简单分析一下，可以发现这是一个$\frac{0}{0}$型极限，要是你手痒痒直接用了，就会陷入绝境：$\text { 原式 }=\lim _{x \rightarrow 0} \frac{2 x \sin \frac{1}{x}-\cos \frac{1}{x}}{1+\cos x}$

实际上这道题的意义就是告诉你要注意洛必达的条件：求导后的极限存在才能用洛必达。

$$\text { 正解：原式 }=\lim _{x \rightarrow 0} \frac{x \sin \frac{1}{x}}{1+\frac{\sin x}{x}}=\frac{0}{2}=0$$

------ 拉格朗日中值定理专区 > 如果函数 $f(x)$ 在闭区间 $[a, b]$ 上连续，在开区间 $(a, b)$ 上可㝵，那么在开区间 $(a, b)$ 内至少存在一点 $\xi$ 使得 : >

f^{\prime}(\xi)=\frac{f(b)-f(a)}

$$这个方法神奇的紧！$$

$$\begin{equation} \lim _{x \rightarrow 0} \frac{\cos (\sin x)-\cos x}{\arcsin ^{4} x} \end{equation}$$

bg

提示：

$$\lim _{x \rightarrow 0} \frac{\cos (\sin x)-\cos x}{\arcsin ^{4} x}=\lim _{x \rightarrow 0} \frac{-\sin \xi \cdot(\sin x-x)}{x^{4}}$$

$\xi$介于$\sin x$ 与$x$之间，由夹逼定理可以得到$\lim_{x\to 0}\frac{\sin \xi}{x}=1$

$$\begin{aligned}&\lim _{x \rightarrow 0} \frac{\cos (\sin x)-\cos x}{\arcsin ^{4} x}\\&=\lim _{x \rightarrow 0} \frac{-(\sin x-x)}{x^{3}}\\&=\lim _{x \rightarrow 0} \frac{1-\cos x}{3 x^{2}}&\\&=\frac{1}{6}\\\end{aligned}$$

驾轻就熟

$$\begin{equation} \lim _{x \rightarrow 0}\left[\frac{a}{x}-\left(\frac{1}{x^{2}}-a^{2}\right) \ln (1+a x)\right](a \neq 0) \end{equation}$$

bg

提示：等价无穷小推论

$$\begin{aligned}&\lim _{x \rightarrow 0}\left[\frac{a}{x}-\left(\frac{1}{x^{2}}-a^{2}\right) \ln (1+a x)\right]\\&=\lim _{x \rightarrow 0}\left[\frac{a}{x}-\frac{\ln (1+a x)}{x^{2}}\right]+\lim _{x \rightarrow 0} a^{2} \ln (1+a x) \\&=\lim _{x \rightarrow 0} \frac{a x-\ln (1+a x)}{x^{2}} \\&=\lim _{x \rightarrow 0} \frac{\frac{1}{2}(a x)^{2}}{x^{2}} {\color{red}\quad\left(🥕-\ln (1+🥕) \sim \frac{1}{2} 🥕^{2}\right)} \\&=\frac{a^{2}}{2} .\end{aligned}$$

$$\begin{equation} \lim _{x \rightarrow+\infty} \frac{\sqrt{\left[(n x)^{n}+1\right]^{n+1}}}{(x+1)\left(x^{2}+2\right) \cdots\left(x^{n}+n\right)} \end{equation}$$

bg

提示：找到相同的项，消消消，提取出来x，凑出来可以计算的无穷小。

$$\begin{aligned}&\lim _{x \rightarrow+\infty} \frac{\sqrt{\left[(n x)^{n}+1\right]^{n+1}}}{(x+1)\left(x^{2}+2\right) \cdots\left(x^{n}+n\right)}\\&=\lim _{x \rightarrow+\infty} \frac{\left(n^{n}+\frac{1}{x^{n}}\right)^{\frac{n+1}{2}}}{\left(1+\frac{1}{x}\right)\left(1+\frac{2}{x^{2}}\right) \cdots\left(1+\frac{n}{x^{n}}\right)}\\&=n^{\frac{n(n+1)}{2}}\end{aligned}$$

$$\begin{equation} \lim_{x\to 0} \frac{x^2(e^x-1)}{\sqrt{1+\tan x}-\sqrt{1+ x}} \end{equation}$$

bg

提示：泰勒展开式

$$\tan x=\sum_{n=1}^{\infty} \frac{B_{2 n}(-4)^{n}\left(1-4^{n}\right)}{(2 n) !} x^{2 n-1}=x+\frac{1}{3} x^{3}+\frac{2}{15} x^{5}+\frac{17}{315} x^{7}+\frac{62}{2835} x^{9}+\frac{1382}{155925} x^{11}+\frac{21844}{6081075} x^{13}+\frac{929569}{638512875} x^{15}+\cdots x \in(-1,1)$$

$$\begin{aligned}&\lim_{x\to 0} \frac{x^2(e^x-1)}{\sqrt{1+\tan x}-\sqrt{1+ x}}\\&=\lim_{x\to 0} \frac{x^3\times(\sqrt{1+\tan x}+\sqrt{1+ x})}{\tan x-x}\\&=\lim_{x\to 0} \frac{x^3\times2}{\tan x-x}\\&=\lim_{x\to 0} \frac{x^3\times2}{\frac{1}{3}x^3}\\&=6\end{aligned}$$

$$\begin{equation} \lim_{x\to 0} \frac{\sqrt{4x^2+x-1}+x+1}{\sqrt{x^2+\sin x}} \end{equation}$$

bg

提示：除以出现次数最多的，最讨厌的那一项。

$$\begin{aligned}&\lim_{x\to 0} \frac{\sqrt{4x^2+x-1}+x+1}{\sqrt{x^2+\sin x}}\\&=\lim _{x \rightarrow \infty} \frac{\sqrt{4+\frac{1}{x}-\frac{1}{x^{2}}}+1+\frac{1}{x}}{\sqrt{1+\frac{\sin x}{x^{2}}}}\\&=\frac{\sqrt{4}+1}{1}\\&=3 \\\end{aligned}$$

$$\begin{equation} \lim _{x \rightarrow 0} \frac{\int_{0}^{x} t \ln (1+t \sin t) \mathrm{d} t}{1-\cos x^{2}} \end{equation}$$

bg

提示：判断极限类型+等价无穷小+洛必达法则

$$\begin{aligned}&\displaystyle \lim _{x \rightarrow 0} \frac{\int_{0}^{x} t \ln (1+t \sin t) \mathrm{d} t}{1-\cos x^{2}}\\&=\displaystyle \lim _{x \rightarrow 0} \frac{\int_{0}^{x} t \ln (1+t \sin t)}{\frac{x^4}{2}} \\&=\displaystyle \lim _{x \rightarrow 0} \frac{x \ln (1+x \sin x)}{2 x^{3}}\\&=\displaystyle\lim _{x \rightarrow 0} \frac{x(x \sin x)}{2 x^{3}}\\&=\frac{1}{2}\end{aligned}$$

$$\begin{equation} \lim _{x \rightarrow+\infty} \frac{\int_{1}^{x}\left(t^{2}\left(\mathrm{e}^{\frac{1}{t}}-1\right)-t\right) \mathrm{d} t}{x^{2} \ln \left(1+\frac{1}{x}\right)} \end{equation}$$

bg

提示：判断极限类型+等价无穷小+洛必达法则

$$\begin{aligned}&\lim _{x \rightarrow+\infty} \frac{\int_{1}^{x}\left(t^{2}\left(\mathrm{e}^{\frac{1}{t}}-1\right)-t\right) \mathrm{d} t}{x^{2} \ln \left(1+\frac{1}{x}\right)}\\&=\lim _{x \rightarrow+\infty} \frac{\int_{1}^{x}\left(t^{2}\left(\mathrm{e}^{\frac{1}{t}}-1\right)-t\right) \mathrm{d} t}{x^{2} \cdot \frac{1}{x}}\\&=\lim _{x \rightarrow+\infty} \frac{\left(\int_{1}^{x}\left(t^{2}\left(\mathrm{e}^{\frac{1}{t}}-1\right)-t\right) \mathrm{d} t\right)^{\prime}}{(x)^{\prime}} \\&=\lim _{x \rightarrow+\infty}\left(x^{2}\left(\mathrm{e}^{\frac{1}{x}}-1\right)-x\right) \qquad \text{令}\ t=\frac{1}{x} \\&=\frac{1}{x} \lim _{t \rightarrow 0^{+}} \frac{\mathrm{e}^{t}-1-t}{t^{2}}\qquad \text{上下都趋近于0，使用洛必达法则} \\&=\lim _{t \rightarrow 0^{+}} \frac{\mathrm{e}^{t}-1}{2 t}\\&=\frac{1}{2}\end{aligned}$$

$$\begin{equation} \lim _{n \rightarrow \infty} \frac{n^{\frac{n^{2}+n+1}{n}}}{(n+1)^{n}}(\sqrt[n]{5}-1) \end{equation}$$

bg

提示：对数字敏感+对公式敏感+剥洋葱法

$$\frac{ a^{🥕}-1}{🥕}\sim \ln a$$

$$\begin{aligned}& \lim _{n \rightarrow \infty} \frac{n^{\frac{n^{2}+n+1}{n}}}{(n+1)^{n}}(\sqrt[n]{5}-1) \\=& \lim _{n \rightarrow \infty} \frac{n^{n+1} \cdot \sqrt[n]{n}}{(n+1)^{n}}(\sqrt[n]{5}-1) \\=& \lim _{n \rightarrow \infty} \frac{n^{n}}{(n+1)^{n}} \frac{\sqrt{5}-1}{1 / n} \\=& \lim _{n \rightarrow \infty} \frac{1}{\left(1+\frac{1}{n}\right)^{n}} \cdot \ln 5 \\=& \frac{\ln 5}{e}\end{aligned}$$

$$\begin{equation} \lim_{x\to 0}\frac{1}{\ln(1+x^2)}-\frac{1}{\sin^2x} \end{equation}$$

bg

提示：对平方差敏感！

$$\begin{aligned}&=\lim _{x \rightarrow 0} \frac{\sin ^{2} x-\ln \left(1+x^{2}\right)}{\sin ^{2} x \ln \left(1+x^{2}\right)} \\&=\lim _{x \rightarrow 0} \frac{\sin ^{2} x-\ln \left(1+x^{2}\right)}{x^{4}} \\&=\lim _{x \rightarrow 0} \frac{\left(\sin ^{2} x-x^{2}\right)-\left[\ln \left(1+x^{2}\right)-x^{2}\right]}{x^{4}} \\&=\lim _{x \rightarrow 0} \frac{(\sin x+x)(\sin x-x)}{x^{4}}-\lim _{x \rightarrow 0} \frac{-\frac{1}{2} x^{4}}{x^{4}} \\&=\lim _{x \rightarrow 0} \frac{(2 x)\left(-\frac{1}{6} x^{3}\right)}{x^{4}}+\frac{1}{2} \\&=-\frac{1}{3}+\frac{1}{2}=\frac{1}{6}\end{aligned}$$

---

泰勒级数求极限专用区

$$\begin{equation} \lim _{x \rightarrow 0} \frac{1+\frac{x^{2}}{2}-\sqrt{1+x^{2}}}{\left(\cos x-e^{x^{2}}\right) \sin x^{2}} \end{equation}$$

bg

提示：基本泰勒展开式

$$\begin{aligned}\sqrt{1+x^{2}} &=\left(1+x^{2}\right)^{\frac{1}{2}}=1+\frac{1}{2} x^{2}+\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)}{2 !} x^{4}+o\left(x^{4}\right) \\&=1+\frac{1}{2} x^{2}-\frac{1}{8} x^{4}+o\left(x^{4}\right) \\& \cos x=1-\frac{x^{2}}{2 !}+o\left(x^{2}\right)=1-\frac{x^{2}}{2}+o\left(x^{2}\right) \\\mathrm{e}^{x^{2}} &=1+x^{2}+o\left(x^{2}\right)\end{aligned}$$

$$\begin{aligned}&\lim _{x \rightarrow 0} \frac{1+\frac{x^{2}}{2}-\sqrt{1+x^{2}}}{\left(\cos x-e^{x^{2}}\right) \sin x^{2}}\\&=\lim _{x \rightarrow 0} \frac{1+\frac{x^{2}}{2}-\left(1+\frac{1}{2} x^{2}-\frac{1}{8} x^{4}+o\left(x^{4}\right)\right)}{\left[\left(1-\frac{x^{2}}{2}+o\left(x^{2}\right)\right)-\left(1+x^{2}+o\left(x^{2}\right)\right)\right] x^{2}} \\&=\lim _{x \rightarrow 0} \frac{\frac{1}{8} x^{4}+o\left(x^{4}\right)}{-\frac{3}{2} x^{4}+o\left(x^{4}\right)}\\&=-\frac{1}{12} \end{aligned}$$

$$\begin{equation} \lim _{n \rightarrow \infty}\left[\left(n^{3}-n^{2}+\frac{n}{2}\right) \mathrm{e}^{\frac{1}{n}}-\sqrt{1+n^{6}}\right] \end{equation}$$

bg

提示：无。😠这谁想得到啊！！!

$$\begin{aligned}&\lim _{n \rightarrow \infty}\left[\left(n^{3}-n^{2}+\frac{n}{2}\right) \mathrm{e}^{\frac{1}{n}}-\sqrt{1+n^{6}}\right]\\&=\lim _{n \rightarrow \infty} n^{3}\left[\left(1-\frac{1}{n}+\frac{1}{2 n^{2}}\right) \mathrm{e}^{\frac{1}{*}}-\sqrt{1+\frac{1}{n^{6}}}\right] \\&\color{red}=\lim _{n \rightarrow \infty} n^{3}\left[\left(1-\frac{1}{n}+\frac{1}{2 n^{2}}\right)-\mathrm{e}^{-\frac{1}{n}} \sqrt{1+\frac{1}{n^{6}}}\right] \\&=\lim _{n \rightarrow \infty} n^{3}\left[\left(1-\frac{1}{n}+\frac{1}{2 n^{2}}\right)-\left(1-\frac{1}{n}+\frac{1}{2 n^{2}}-\frac{1}{3 !} \frac{1}{n^{3}}+o\left(\frac{1}{n^{3}}\right)\right)\left(1+o\left(\frac{1}{n^{3}}\right)\right)\right] \\&=\frac{1}{6}\end{aligned}$$

蓦然回首

$$\begin{equation} \lim _{x \rightarrow 0} \frac{\left(2+\sin x^{2}\right)^{x}-2^{\sin x}}{x^{3}} \end{equation}$$

bg

提示：努力拼凑出来等价无穷小，提取相同的项，

$$\begin{aligned}&\lim _{x \rightarrow 0} \frac{\left(2+\sin x^{2}\right)^{x}-2^{\sin x}}{x^{3}}\\&=\lim _{x \rightarrow 0} \frac{\left(2+\sin x^{2}\right)^{x}-2^{x}}{x^{3}}+\lim _{x \rightarrow 0} \frac{2^{x}-2^{\sin x}}{x^{3}} \\&=\lim _{x \rightarrow 0} \frac{2^{x}\left[\left(1+\frac{\sin x^{2}}{2}\right)^{x}-1\right]}{x^{3}}+\lim _{x \rightarrow 0} \frac{2^{\sin x}\left(2^{x-\sin x}-1\right)}{x^{3}} \\&=\lim _{x \rightarrow 0} \frac{\frac{\sin x^{2}}{2} \cdot x}{x^{3}}+\lim _{x \rightarrow 0} \frac{(x-\sin x) \ln 2}{x^{3}} \\&=\lim _{x \rightarrow 0} \frac{\frac{1}{2} x^{3}}{x^{3}}+\lim _{x \rightarrow 0} \frac{\left(\frac{1}{6} x^{3}\right) \ln 2}{x^{3}} \\&=\frac{1}{2}+\frac{\ln 2}{6}\\\&=\frac{1}{2}+\ln \sqrt[6]{2} \end{aligned}$$

$$\begin{equation} \lim _{x \rightarrow 1} \frac{x-x^{x}}{1-x+\ln x} \end{equation}$$

bg

提示：努力拼凑出来等价无穷小，提取相同的项，

• 解法一
• 解法二

用换元法把趋向于1的x转换成趋向于0的h，多次拼凑并利用等价无穷小。

$$\begin{aligned}&\lim _{x \rightarrow 1} \frac{x-x^{x}}{1-x+\ln x} \\&=\lim _{h \rightarrow 0} \frac{(1+h)\left[1-(1+h)^{h}\right]}{\ln (1+h)-h} \\&=\lim _{h \rightarrow 0} \frac{e^{h \ln (1+h)}-1}{h-\ln (1+h)} \\&=\lim _{h \rightarrow 0} \frac{h \ln (1+h)}{h-\ln (1+h)} \\&=\lim _{h \rightarrow 0} \frac{h^{2}}{h-\ln (1+h)} \\&=\lim _{h \rightarrow 0} \frac{2 h}{1-\frac{1}{1+h}} \\&=2 \lim _{h \rightarrow 0}(1+h) \\&=2 \end{aligned}$$

往死里凑等价无穷小！！！

$$\begin{aligned}&\lim _{x \rightarrow 1} \frac{x-x^{x}}{1-x+\ln x} \\&=\lim _{x \rightarrow 1} \frac{-x\left[\mathrm{e}^{(x-1) \ln x}-1\right]}{\ln{[1+(x-1)]}-(x-1)]}\\&=\lim _{x \rightarrow 1} \frac{-(x-1) \ln x}{-\frac{1}{2}(x-1)^{2}} \\&=2 \lim _{x \rightarrow 1} \frac{(x-1) \ln {[1+(x-1)]}}{(x-1)^{2}}\\&= 2 \lim_{x\to 1} \frac{(x-1)^2}{(x-1)^2}\\&=2\\\end{aligned}$$

$$\begin{equation} \lim _{x \rightarrow+\infty}\left[\sqrt[3]{x^{3}+x^{2}+x+1}-\sqrt{x^{2}+x+1} \frac{\ln \left(\mathrm{e}^{x}+x\right)}{x}\right] \end{equation}$$

bg

提示：要先推演一番，才能做出来😂

$$\color{blue} \lim _{x \rightarrow+\infty} \frac{\ln \left(\mathrm{e}^{x}+x\right)}{x}=\lim _{x \rightarrow+\infty} \frac{\ln \left[\mathrm{e}^{x}\left(1+\frac{x}{\mathrm{e}^{x}}\right)\right]}{x}=1+\lim _{x \rightarrow+\infty} \frac{\ln \left(1+\frac{x}{\mathrm{e}^{x}}\right)}{x}$$

$$\begin{aligned}& \lim _{x \rightarrow+\infty}\left[\sqrt[3]{x^{3}+x^{2}+x+1}-\sqrt{x^{2}+x+1} \frac{\ln \left(\mathrm{e}^{x}+x\right)}{x}\right]\\=& \lim _{x \rightarrow+\infty}\left(\sqrt[3]{x^{3}+x^{2}+x+1}-\sqrt{x^{2}+x+1}\right)-\lim \frac{\sqrt{x^{2}+x+1}}{x \rightarrow+\infty} \ln \left(1+\frac{x}{\mathrm{e}^{x}}\right) \\=& \lim _{x \rightarrow+\infty} x\left(\sqrt[3]{1+\frac{1}{x}+\frac{1}{x^{2}}+\frac{1}{x^{3}}}-\sqrt{1+\frac{1}{x}+\frac{1}{x^{2}}}\right)-0 \\=& \lim _{x \rightarrow+\infty} x\left(\sqrt[3]{1+\frac{1}{x}+\frac{1}{x^{2}}+\frac{1}{x^{3}}}-1\right)-\lim _{x \rightarrow+\infty} x\left(\sqrt{1+\frac{1}{x}+\frac{1}{x^{2}}-1}\right) \\=& \lim _{x \rightarrow+\infty} x\left[\frac{1}{3}\left(\frac{1}{x}+\frac{1}{x^{2}}+\frac{1}{x^{3}}\right)\right]-\lim _{x \rightarrow+\infty} x\left[\frac{1}{2}\left(\frac{1}{x}+\frac{1}{x^{2}}\right)\right] \\=& \frac{1}{3}-\frac{1}{2}\\=&-\frac{1}{6} \end{aligned}$$

$$\begin{equation} \lim _{x \rightarrow 0} \frac{\int_{0}^{x^{2}} f(t) \mathrm{d} t}{x^{2} \int_{0}^{x} f(t) \mathrm{d} t}\quad f(0)=0,f'(0)\ne 0 \end{equation}$$

bg

提示：使用了两次洛必达法则（标蓝部分），以及导数的定义（精妙之处）

$$\begin{aligned}& \lim _{x \rightarrow 0} \frac{\int_{0}^{x^{2}} f(t) \mathrm{d} t}{x^{2} \int_{0}^{x} f(t) \mathrm{d} t}\\&={\color{blue} \lim _{x \rightarrow 0} \frac{2 x f\left(x^{2}\right)}{2 x \int_{0}^{x} f(t) \mathrm{d} t+x^{2} f(x)}} \\&=\lim _{x \rightarrow 0} \frac{2 f\left(x^{2}\right)}{2 \int_{0}^{x} f(t) \mathrm{d} t+x f(x)} \\&=\color{blue} \lim _{x \rightarrow 0} \frac{4 x f^{\prime}\left(x^{2}\right)}{3 f(x)+x f^{\prime}(x)} \\&=\lim _{x \rightarrow 0} \frac{4 f^{\prime}\left(x^{2}\right)}{\frac{3 f(x)}{x}+f^{\prime}(x)} \\&=\color{purple} \frac{4 f^{\prime}(0)}{3 f^{\prime}(0)+f^{\prime}(0)} \\&=1\end{aligned}$$

$$\begin{equation} \text { 设函数 } f(x) \text { 可导, 求极限 } \lim _{x \rightarrow x_{0}} \frac{x_{0} f(x)-x f\left(x_{0}\right)}{x-x_{0}} \end{equation}$$

bg

提示：使用导数的定义，尽力去凑导数定义式的形式，另外，值得注意的是：可导不代表着该函数在任意点处的极限都存在

$$\begin{aligned}&\lim _{x \rightarrow x_{0}} \frac{x_{0} f(x)-x f\left(x_{0}\right)}{x-x_{0}}\\&=\lim _{x \rightarrow x_{0}} \frac{x_{0} f(x)-x_{0} f\left(x_{0}\right)}{x-x_{0}}-\lim _{x \rightarrow x_{0}} \frac{x f\left(x_{0}\right)-x_{0} f\left(x_{0}\right)}{x-x_{0}} \\&=x_{0} \lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}-f\left(x_{0}\right) \\&=x_{0} f^{\prime}\left(x_{0}\right)-f\left(x_{0}\right)\end{aligned}$$

经验总结

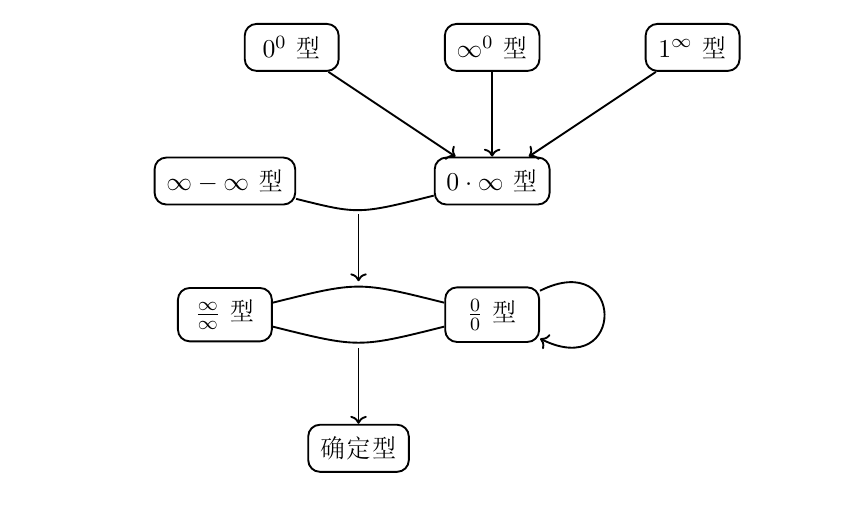
对于求极限问题，首先要判断所求极限的类型，若属于确定型，就按确定型中具体类型进行计算；若属于待定型，则看属于待定型中的“商型”、“积差型”还是“幂指型”，其中“商型”是最基础的待定型，“积差型”和“幂指型”都要经过转化最终转化为“商型”进行计算，其中，$1^∞$ 型除了可以转化为“商型”进行计算外，还可以利用第二重要极限的推广进行计算。确定所求极限的类型至关重要，只有知道所求极限的类型了，才可以按照相应类型的方法进行计算。^[2]

等价无穷小要义

当$🥕 \to 0$时

🥕相当于一个函数，最常见的的就是$x$了

$$🥕 \sim \sin{(🥕)}\sim \tan{(🥕)}\sim {\color{red} e^{🥕}-1} \sim \ln(1+🥕)\sim \arcsin{(🥕)}\sim \arctan{(🥕)}$$

$$1-\cos{(🥕)} \sim \frac{1}{2}🥕^2 \qquad \qquad 🥕-\sin{(🥕)} \sim \frac{1}{6}🥕^3$$

$$\color{blue} 1-\cos{(🥕)} \sim \frac{1}{2}🥕^2\Longrightarrow 1-n\cos(🥕) \sim\frac{n}{2}x^2-n+1$$

$$\ln(🥕+\sqrt{1+🥕^2})\sim🥕$$

$$\color{blue}\ln(1+🥕)\sim 🥕 \Longrightarrow \log_🥬(1+🥕)\sim \frac{🥕}{\ln 🥬}$$

$$\color{blue}e^{🥕}-1\sim 🥕 \Longrightarrow 🥬^{🥕}-1\sim 🥕\ln 🥬$$

$$(1+🥕)^🥬-1 \sim 🥬🥕\qquad \frac{ 🥬^{🥕}-1}{🥕}\sim \ln 🥬$$

加减法使用等价无穷小^[3]

口诀： 加不反，减不同，等价随便换

若 $\alpha \sim \alpha^{\prime}, \beta \sim \beta^{\prime}$, 且 $\lim \frac{\alpha}{\beta}=A \neq-1$, 则 $\alpha+\beta \sim \alpha^{\prime}+\beta^{\prime}$;

若 $\alpha \sim \alpha^{\prime}$, $\beta \sim \beta^{\prime}$, 且 $\lim \frac{\alpha}{\beta}=A \neq 1$, 则 $\alpha-\beta \sim \alpha^{\prime}-\beta^{\prime}$.

*等价无穷小的推导

此部分从属于紫晶计划·铁石 笔尖学术

泰勒展开式

泰勒级数（英语：Taylor series）用无限项连加式——级数来表示一个函数，这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒（Sir Brook Taylor）来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做麦克劳林级数（英语：Maclaurin series），以苏格兰数学家科林·麦克劳林的名字命名^[4]。所以，我们经常用的所谓的“泰勒展开式”实际上应该称为“麦克劳林级数”。

刚才差点又陷入误区，准备把无穷级数全部复习一遍，之后再来写这篇文章。实际上，很多东西，只有很少一部分是关键所在，理解了关键，就没有必要从头再来。况且，兴致是会消减的，学着学着就把写文章的激情磨光了，这可能也是多巴胺的规律之一吧。所以本文就从关键开始，从核心开始，以紫晶计划的要义“取其精华，弃其糟粕。”为指导，把我想表达的表达出来。

本文的主要依据是泰勒级数，泰勒级数的标准形式为：

$${\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}}={\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots }$$

以下为常见的麦克劳林展开式（不要怕，只需要记住五个我标注为$\color{purple}\text{紫色的}$，就足以推导出大多数等价无穷小）：

bg

$$\begin{aligned}&{\displaystyle {\color{red}\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+\cdots +x^{n}+\cdots \quad \forall x:\left|x\right|<1}\\&{\displaystyle{ \color{purple}(1+x)^{\alpha }}=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}=1+\alpha x+{\frac {\alpha (\alpha -1)}{2!}}x^{2}+\cdots +{\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}x^{n}+\cdots }\quad{\displaystyle \forall x:\left|x\right|<1,\forall \alpha \in \mathbb {C} }\\&{\displaystyle {\color{purple} e^{x}}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}+\cdots \quad \forall x}\\&{\displaystyle {\color{teal} a^{x}}=e^{x \ln a}=\sum _{n=0}^{\infty }{\frac {(x \ln a)^{n}}{n!}}=1+x \ln a+{\frac {(x \ln a)^{2}}{2!}}+{\frac {(x \ln a)^{3}}{3!}}+\cdots +{\frac {(x \ln a)^{n}}{n!}}+\cdots \quad \forall x}\\& {\displaystyle {\color{red} \ln(1-x)}=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots -{\frac {x^{n}}{n}}-\cdots \quad \forall x\in [-1,1)} \\&{\displaystyle{\color{purple} \ln(1+x)}=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots +{\frac {(-1)^{n+1}}{n}}x^{n}+\cdots \quad \forall x\in (-1,1]} \\&{\displaystyle{\color{teal} \log_a(1+x)}=\frac{\ln (1+x)}{\ln a}=\frac{1}{\ln a}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=\frac{x}{\ln a}-{\frac {x^{2}}{2{\ln a}}}+{\frac {x^{3}}{3{\ln a}}}-\cdots +{\frac {(-1)^{n+1}}{n{\ln a}}}x^{n}+\cdots \quad \forall x\in (-1,1]} \\\end{aligned}$$

$${\displaystyle {\begin{aligned}\color{purple} \sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&\forall x\\[6pt]\color{red} \cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&\forall x\\[6pt]\color{purple} \tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&\forall x:|x|<{\frac {\pi }{2}}\\[6pt]\color{red} \sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots &&\forall x:|x|<{\frac {\pi }{2}}\\[6pt]\color{red} \arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&\forall x:|x|\leq 1\\[6pt]\color{red} \arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}+\cdots &&\forall x:|x|\leq 1\\[6pt]\color{red} \arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&\forall x:|x|\leq 1,\ x\neq \pm i\end{aligned} }}$$

等价运算符

此部分为本人杜撰，结论不够准确严谨，但应付等价无穷小的推导应该绰绰有余。如有错误，还望指正🐰。

等价无穷小的不严格定义：

当$x\to 0$时，两个函数$A(x),B(x)$同时收敛于一个常数(英文：constant) $C$，那么这两个函数为$x\to0$时等价无穷小，记作$A(x)\sim B(x)$

下面介绍一下等价无穷小运算符"$\sim$"的运算规律，当$x\to 0$时，有如下运算规律：

1. $$if\ A(x)\sim B(x),B(x)\sim C(x)\quad then\ \color{red} A(x) \sim C(x)$$

2. $$if\ A(x)\sim B(x),C\ is\ a\ constant,\ then \$$

   $$\color{red} A(x)\cdot C \sim B(x)\cdot C$$

   $$\color{red} A(x)\pm C \sim B(x)\pm C$$

3. $$if\ A(x)\sim a\ , B(x)\sim b$$

   $$\color{red} A(x) \cdot B(x) \sim a \cdot b$$

   $$\color{red} \frac{A(x)}{ B(x)} \sim \frac{a}{b}$$

   $$\color{red} A(x) + B(x) \sim a +b\quad if\ and\ only\ if\ \lim_{x\to0}\frac{A(x)}{B(x)}\ne -1$$

   $$\color{red} A(x) - B(x) \sim a - b\quad if\ and\ only\ if\ \lim_{x\to0}\frac{A(x)}{B(x)}\ne 1$$

   值得注意的是，对于$\color{red}A(x)-B(x)$这种情形，往往会出现$\displaystyle \lim_{x\to0}\frac{A(x)}{B(x)}= 1$, 这个时候可以利用下文所讲的泰勒展开式来进行等价😎

4. 当函数$A(x)$在$x\to 0$处，收敛于某一值，且其可以展开为如下的多项式$a_0+a_1x+a_2x^2+\cdots a_nx^n$，则：$\color{red} A(x) \sim a_0+a_1x+a_2x^2+\cdots a_nx^n$

   推论1：这个和高阶等价无穷小有关，应该有更严谨的表达，但鄙人懒得翻了，就按我的意思表达吧。

   $$When\ A(x) = a_0+a_1x+a_2x^2+\cdots a_nx^n,\ B(x)=b_0+b_1x+b_2x^2+\cdots+b_nx^n\ then \\ \lim_{x\to 0}\frac{A(x)}{B(x)}=\frac{a_0+a_1x+a_2x^2+\cdots a_nx^n} {=b_0+b_1x+b_2x^2+\cdots+b_nx^n}\ \color{teal} if \ n<m$$

   推论2：泰勒展开式移项$\color{red} A(x)-a_0-a_1 x- \cdots a_j x^j \sim \color{blue} a_{j+1}x^{j+1}+\cdots a_n x^n$

等价无穷小·推导Plus+Pro

泰勒展开式等价无穷小

由于较高阶次的项，考试也不会考，写下来也麻烦的紧，这里就利用最高次幂为二或三的展开式来推导常见的无穷小。

$${\displaystyle {\begin{aligned} \color{purple} \sin x\quad&\sim x &&\sim x-{\frac {x^{3}}{6}}\\[6pt] \color{purple} \arcsin x\quad&\sim x &&\sim x+{\frac {x^{3}}{6}}\\[6pt] \color{purple} \tan x\quad&\sim x &&\sim x+{\frac {x^{3}}{3}}\\[6pt] \color{purple} \arctan x\quad&\sim x &&\sim x-{\frac {x^{3}}{3}}\\[6pt] \color{purple} \cos x\quad&\sim 1 &&\sim 1-{\frac {x^{2}}{2}}\\[6pt] \color{purple} e^x\quad&\sim 1 &&\sim 1+x &&\sim 1+x+{\frac {x^{2}}{2}}\\[6pt] \color{teal} a^x\quad&\sim 1 &&\sim 1+x \ln a &&\sim 1+x \ln a+{\frac {(x \ln a)^{2}}{2}} \\[6pt] \color{purple} \ln(1+x)\quad&\sim x &&\sim x-{\frac {x^{2}}{2}}\\[6pt] \color{teal} \log_a(1+x)\quad&\sim\frac{x}{\ln a} &&\sim\frac{x}{\ln a}-{\frac {x^{2}}{2{\ln a}}}\\[6pt] \color{purple} (1+x)^a\quad&\sim 1 &&\sim 1+ax &&\sim 1+ax+\frac{a(a-1)}{2}x^2 \\[6pt] \color{purple} \frac{1}{1+x}\quad&\sim 1 &&\sim 1-x &&\sim 1-x + x^2 \\[6pt] \color{purple} \frac{1}{1-x}\quad&\sim 1 &&\sim 1+x &&\sim 1+x + x^2 \\[6pt] \end{aligned}}}$$

这些是原始的等价无穷小，亦可以看作出题者的后台,亦可以看作出题者的后台,#000000,#000000

根据等价运算符的运算规律，特别是推论2，我们可以很容易得到以下推论：

$$x \sim {\color{blue} \sin{(x)}}\sim \tan{(x)}\sim {\color{blue} e^{x}-1} \sim \ln(1+x)\sim {\color{blue} \arcsin{(x)}}\sim \arctan{(x)}$$

$${\displaystyle {\begin{aligned} \color{purple} \sin x-x\quad&\sim -{\frac {x^{3}}{6}}\\[6pt] \color{purple} \arcsin x-x\quad&\sim {\frac {x^{3}}{6}}\\[6pt] \color{purple} \tan x-x\quad&\sim {\frac {x^{3}}{3}}\\[6pt] \color{purple} \arctan x-x \quad&\sim -{\frac {x^{3}}{3}}\\[6pt] \color{purple} \cos x-1\quad&\sim -{\frac {x^{2}}{2}}\\[6pt] \color{purple} e^x-1\quad&\sim x &&\sim x+{\frac {x^{2}}{2}}\\[6pt] \color{teal} a^x-1\quad&\sim x \ln a &&\sim x \ln a+{\frac {(x \ln a)^{2}}{2}} \\[6pt] \color{purple} \ln(1+x)-x\quad&\sim -{\frac {x^{2}}{2}}\\[6pt] \color{teal} \log_a(1+x)-\frac{x}{\ln a}\quad&\sim-{\frac {x^{2}}{2{\ln a}}}\\[6pt] \color{purple} (1+x)^a-1\quad&\sim ax &&\sim ax+\frac{a(a-1)}{2}x^2 \\[6pt] \color{purple} \frac{-x}{1+x}\quad&\sim -x &&\sim -x + x^2 \\[6pt] \color{purple} \frac{x}{1-x}\quad&\sim x &&\sim x + x^2 \\[6pt] \end{aligned}}}$$

等价无穷小·推导 50

通过核心公式（泰勒展开式中标紫的地方）：$\sin x,\tan x, e^x, \ln(x+1)$，加上简单的加减乘除，三角函数运算，对数运算，以及上文的等价运算，可以很方便的推导出其他的等价无穷小，太累了，过程省略，给你张图，慢慢推导吧

---

1. 维基百科编者. 洛奇[G/OL]. 维基百科. 中文名：《洛奇》，一部1976年的美国电影，由约翰·艾维森执导，西尔维斯特·史泰龙编剧兼主演，讲述一个籍籍无名的拳手洛奇·巴尔博亚在获得与世界重量级冠军阿波罗·奎迪争夺冠军的机会后奋力一搏的美国梦故事。 ↩︎

2. 王琦, 尤卫玲, 谭志明. 求极限刍议[J]. 应用数学进展, 2020, 9(5): 682-687. ↩︎

3. 黄星,张倩瑶.利用等价无穷小替换求极限时应注意的问题J.黑龙江科学,2021,12(13):130-131 ↩︎

4. 维基百科编者. 泰勒级数[G/OL]. 维基百科, 2022(20220324)[2022-03-24]. ↩︎